블로그

오랜만에 포스팅합니다.  

제 블로그가 조금이라도 도움이 되신다고 생각하셔서..방문해 주시는 학생분들의 '바램?'을 생각한다면 시험기간중 범위에 맞춰드리는 것이 이왕 하는 블로그 더 여러분들께 큰 도움이 될 수 있을텐데...라는 죄송한 마음이 듭니다. 각설하고..길게 보고 성실히 가겠습니다.

1. 부정적분과 정적분 : 뉴튼과 라이프니츠   - 과연 누가 먼저 미적분을 발견했을까?

부정정분(不定積分)

정(定)해지지 않은 적분을 의미합니다. 무엇이 정해지지 않았을까요? '적분값'이 정확하게 정해지지 않은 적분입니다. 이게 무슨 말이죠? 적분값이 정확하게 정해지지 않다니요? 나중에 보시면 아시겠지만 부정적분은 F(x)(원시함수)+C인데..여기서 상수 C가 무수히 많아 정확하게 정의되지 않습니다.

영어로는 indefinite integral !

definite는 무엇을 정의한다는 뜻이죠? 영어로도 indefinite integral은 정확하게 정의되지 않은 적분을 의미합니다. 결론적으로 부정적분은 '정확한 적분값이 아닌 원시함수, 도형에 적용하면 어떤 함수의 그래프가 만들어 내는 도형의 넓이나 부피를 구할 수 있는 일반적인 식' 이라 말씀드릴 수 있겠습니다. 

반면에 정적분은 범위를 정한 definite integral을 의미합니다. 범위를 정했기 때문에 구체적인 값을 정의할 수 있습니다. (그러고 보면 define이란 영어의 어원 자체도 수학적 사고같습니다.^^ fine은 정제하다라는 뜻이 있구요..de는 세밀하게? 꼼꼼하게? ^^)

일반적인 사각형의 넓이는 '밑변×높이'라고만 말할 수 있습니다.

하지만 밑변이 4cm, 높이가 5cm인 사각형의 넓이는 20cm²라고 구체적으로 말할 수 있습니다.

부정적분과 정적분의 차이입니다.

요즘 여러분이 배우는 미적분은 거의 모두 라이프니츠의 미적분입니다.

뉴튼은 물리학의 속도과 운동을 연구하던 중 미적분을 발견해 냈습니다. 이름도 미적분이 아닌 유율법(method of fluxions)이라 붙였습니다.(후에 이 유율법으로 만유인력의 법칙을 완성합니다.) 뉴튼의 미적분은 '함수의 적분은 단순히 미분하는 연산의 역연산'이라는 직관적인 통찰력에 기초를 두고 있습니다. 즉, 뉴튼의 미적분은 넓이, 접선, 곡선의 길이, 함수의 최대 최소 구하기 같은..기존에 이미 발견된 전혀 다른 영역의 공식들을 통합하는 간단한 해석적 해법의 일환이었던 것입니다. 간단히 비유하자면 거리/시간=속도이고..이 속도는 운동에 지대한 영향을 미친다. 이렇게 거리함수를 시간으로 나눈 것을 미분함수라고 한다면 미분함수를 역연산하면 다시 거리함수가 되지 않겠는가? 이 것이 적분이다.

여기서 역연산이란 아래와 같은 의미입니다.

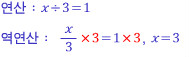
x를 구하기 위해 나누기 3의 역연산인 곱하기 3을 이용했습니다.

그렇다면

거리함수 f(x)/시간 = 속도함수 f'(x)

속도함수 f'(x)×시간=거리함수 f(x)라고 할 수 있겠죠?

나누기 시간의 '역연산'을 이용하여 원래의 함수인 거리함수를 구했고 이를 적분이라고 본 것입니다. 뉴튼은..

그럼 라이프니츠의 미적분들 볼까요?

라이프니츠의 미분은 곡선의 접선 또는 함수의 극대 극소를 찾는 과정에서 발견한 것입니다. (어? 우리가 배운 미분내용과 같네요?)

대포에서 포탄을 쏘았을 때 그 포탄이 그리는 곡선의 두 점을 지나는 직선을 생각해봅시다.

두 점의 거리를 매우 짧게 하면(아..여기서 극한의 개념도 나오는 군요..순간 변화율!) 직선은 그 순간 포탄이 날아가는 방향을 나타내게 되겠죠. 이 직선이 수평과 평행한 곳에서 포탄의 높이는 가장 높고(극대점) 이후 점점 떨어지게 됩니다. 따라서 이 직선이 수평으로 된 곳만 찾으면  그 포탄의 최고 높이를 구할 수 있다는 것입니다. 완전 우리가 배운 미분과 똑 같습니다. 접선도 그렇습니다. 이 두 점사이의 거리를 점점 0에 가깝게 하면 직선은 사실상 곡선과 한 점에서 만나게 되는 것과 같은 효과입니다. 이를 접선이라고 하였습니다. 

라이프니츠는 이 원리를 이용하여 어떤 함수가 만들어내는 도형의 넓이나 부피도 구했습니다. 밑변을 0에 가깝게 작게 하여...dx죠...함수값 f(x)는 높이구요..높이×밑변, f(x)×dx...우리가 배운 구분구적법입니다. 

그렇습니다. 우리가 배운 미적분은 오히려 라이프니츠의 개념에 더 가까운 것들이었습니다. 

그리고 인테그랄 기호도 라이프니츠가 만든 기호이고, 이는 잘게 쪼갠 사각형을 더한다는 sum이 s자를 길게 늘인 것입니다. 

결코 쉬어가는 내용이 아니라구요? ^^

오히려 이렇게 폭넓게 개념의 탄생 배경과 역사도 공부하시는 것이 진정한 개념에 충실한 수학공부랍니다. ^^ 

그럼..본격적으로 부정적분부터 살펴보겠습니다.

2. 부정적분의 의미 : 어떤 함수 f(x)의 부정적분은 무수히 많다. 상수 C 때문에...

수2에서 미분을 배웠죠..어떤 함수 f(x)의 도함수를 f'(x)라고 했고, 이를 미분함수라고 불렀습니다. 이제 반대로! 역으로! ... f'(x)는 어떤 함수를 미분했길래 나온 함수였나요? 네..맞습니다. f(x)입니다.

y=x²이라는 함수를 미분하면 y'=2x입니다. 그리고2x는 x²을 미분했길래 나온 함수입니다.

이제 미분했던 전과정을 잊어버리시고..역과정만 새로운 판에서 생각해 봅시다.

2x를 f(x)라고 봅시다. 그럼 x²은요? 미분하면 f(x)인 2x가 되는 x²은 무엇이라 부를까요? 원시함수라 부릅니다. 그리고 이 원시함수를 찾는 역미분과정을 우리는 적분과정이라 합니다.

미분하여 f(x)가 되는 함수 를 함수 f(x)의 부정적분(또는 원시함수)  F(x)라 합니다.

그리고 어떤 함수 f(x)의 부정적분 F(X)는 수 없이 많습니다. 상수 때문입니다.

x²+1, x²+2, x²+3 , x²+4 ...... 미분하면 모두 2x입니다.

이는 역으로 2x의 부정적분은 상수까지 정확하게 짚어낼 수는 없다는 의미와도 같지요

그냥...무한한 상수를 일반상수 C로 표시하여 F(x)+C 로 나타낼 수 밖에 없습니다.

          해석) 미분하여 f(x)가 되는 함수는 F(x)+C이다. ( F(x)+C를 미분하면 f(x)가 된다. )

          표현) 함수 f(x)의 역미분과정은  ∫f(x)dx이다.

                   함수 f(x)의 부정적분(원시함수)은 F(x)+C이다.

위치(거리)는 속도×시간이었죠?

시간이야 머..당연하게 흘러가는 독립변수이고,

속도는 두 가지 케이스가 있습니다. 시간이 지날 수록 변하는 속도와 변하지 않는 일정한 속도..

변하는 속도는 v(t)= t m/sec의 간단한 일차함수로 생각할 수 있고

변하지 않는 일정한 도는 v(t)=10 m/sec와 같은 상수 함수로 생각할 수 있습니다. 

 

그럼 10초 후의 위치를 구해 볼까요? '속도×시간'인 위치를...

일정한 속도로 달린 10초 후의 위치는 10×10=100m입니다.

그럼 변하는 속도로 달린 10초후의 위치는 어디쯤일까요?(직선으로 움직인다고 가정합시다)

 

잘 안 떠오르시죠? 속도가 일정치 않기 때문입니다. 위치는 속도×시간인데...이 속도가 매 초마다 변하므로 쉽게 구할 수 없습니다.

 

그러나..우리는 그래프로 이해하면 이를 쉽게 해결할 수 있습니다.

 

일단 일정한 속도로 달린 10초후의 위치는 아래의 그래프에서 직사각형의 넓이가 됩니다. 속도×시간이 직사각형의 밑변×높이가 되기 때문입니다.

 

 

그럼 변하는 속도의 그래프를 볼까요?

 

아...삼각형의 넓이가 되겠군요..10×10×0.5=50m가 움직인 거리군요..

그.런.데...삼각형이 아닌 속도함수라면? 이차함수이거나..삼차함수이거니..

고민입니다.

그래서 다시 삼각형을 들여다 봅니다.

혹시 이 위치(넓이)를 매 초마다 계산한다면 어떠할까?

복잡한 속도함수의 위치(넓이)도 구할 수 있지는 않을까?

매 초마다 자동차 계기판을 들여다보면서 움직인 위치를 확인하는 겁니다.

매 초마다 넓이를 계산하는 겁니다.

아래와 같이요..

 

작은 직사각형들이 매 초마다 움직인 위치(넓이)를 나타내는 것입니다.

물론...빈 틈이 보이지요...오차입니다.

하지만..매초가 아닌..0.1초, 0.01초...즉, 계기판을 들여다 보는 시간(interval)을 좁힌다면 이 빈 틈(오차)는 거의 작아질 것입니다. 삼각형의 넓이와 거의 동일해 지겠지요(여기서 극한의 개념이 필요합니다.)

 

이제..임의의 수 t로 변환하여 속도함수와 위치함수를 볼까요?

속도함수는 위에서 본 바와 같이  v(t)= t 이구요

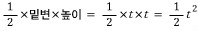위치함수는..입니다.

매 시간마다의 위치를 알려주는 새로운 함수 '위치함수'입니다.

(면적이 위치함수라는 함수로 바뀌어지는 순간입니다.)

 

그럼..속도함수와 위치함수간 관계를 볼까요?

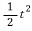위치함수 을 미분하면 속도함수 t가 됩니다.

그리고 이러한 관계는 속도함수가 일차함수가 아닌 이차함수, 삼차함수에서도 동일하게 적용되는 것을 뉴턴은 발견했습니다.

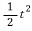그럼..속도함수 t를 역미분하면 무엇이 나와야 할까요? 예..맞습니다. 위치함수 이 나와야 합니다. 그리고...이 t를 역미분한 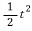은 그래프의 넓이였습니다. 넓이...

만약 이 넓이가 만약 매우 잘게 쪼갠 사각형들을 모아서 구한 넓이라면 이를 우리는 '적분'이라 부립니다. 積(쌓을 적)...잘게 나누는 分...합쳐서 적분입니다. 잘게 나누어 쌓는 것이죠..오차가 없는 넓이를 구하기 위해서요.. 

 

이제 우리는 역미분 과정이 적분으로 연결되는 연결고리가 무엇인지를 알게 되었습니다.

바로..그래프의 넓이이지요...

 

그래서 여러분의 교과서가 부정적분(역미분), 구분구적법(그래프의 넓이), 정적분 순서로 연결되어 챕터가 구성되어 있는 것이랍니다.

 

다시 한 번 반복합니다.

 

위치함수를 미분하면 속도함수가 나오고

속도함수를 역미분하면 위치함수가 나온다!

그리고 그 역미분 과정은 그래프의 넓이를 구하는 과정인 적분이라 이름 붙일 수 있다. 

 

이상이 뉴턴이 고민했던 내용들입니다.

부정적분 상수 C에 대해 조금 다른 각도에서 살펴볼까요? 기하학적인 각도에서 말이죠

F(x)+C 함수를 미분하면 도함수 f(x)가 된다는 것은 이제 아셨죠?

그리고..도함수 f(x)은 접점에서의 순간기울기, 접선의 기울기인 것도 아시고 계시죠?

그럼 아래 그래프의 의미를 온 몸으로 느끼실 수 있으셔야 합니다. ^^

y=F(x)를 수직방향으로 위 아래로 이동해도 어떤 점 x에서이 순간기울기는 바뀌지 않습니다.

즉, F(x)+C1나 F(x)+C2나 F(x)+C3나...

어떤 점 x에서의 순간기울기는 모두 같습니다. 모두 f(x)입니다.

어떤 점 x에서의 접선의 기울기는 모두 같습니다. 모두 f(x)입니다.

어떤 점 x에서의 도함수는 모두 같습니다. 모두 f(x)입니다. 

즉, F'(x)=f(x)이면 f(x)의 부정적분 원시함수 그래프는 F(x)를 y축으로 평행이동 시킨 무한히 많은 함수들입니다.  

연습문제

1. 다음 등식을 만족하는 함수 f(x)를 구하시오

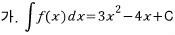
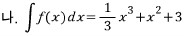
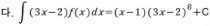
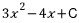가. f(x)를 적분하면 이므로, 역으로 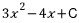을 미분하면 f(x)이다.

    답 : 6x-4

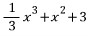나. f(x)를 적분하면 이므로, 역으로 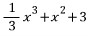을 미분하면 f(x)이다.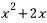

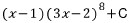    답 :

다. (3x-2)f(x)를 적분하면 이므로, 역으로 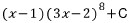을

     미분하면 (3x-2)f(x)이다.

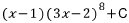     의 미분은 우선 '곱의 미분법'을 쓰고,  '합성함수의 미분법'도 사용할 

     줄 알아야 한다.

     미분하면

     =

     =

 

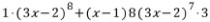
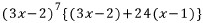
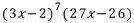
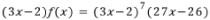     이므로

    

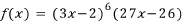
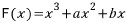2. 함수 가 함수 f(x)의 부정적분 중 하나이고, f(0)=3, f'(0)=1일 때, 상수 a, b의 곱 ab를 구하시오

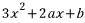F(x)를 미분한 가 f(x)이고, f'(x)는 이를 또 미분한 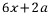이다.

f(0)=b=3

f'(0)=2a=1, a=1/2

따라서 ab=3/2